| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- UnMineable
- 범용인증서갱신
- 범용인증서최저가
- 법인범용인증서
- 이더 채굴
- 전자서명보안토큰 비밀번호 분실
- 법인범용공동인증서
- 법인설립주의사항
- 법인등기온라인
- 일인법인
- 가정 채굴
- 지문인식토큰
- 법인등기인터넷
- 범용인증서가격
- 홈채굴
- 채굴량 높이기
- 조달청인증서
- 1인법인 은행
- 보안토큰 비밀번호 분실
- 비트 채굴
- 보안토큰 초기화
- 법인관외이전
- 전자서명 비밀번호 초기화
- 애프터버너 국민 세팅 값
- 법인범용인증서갱신
- 채굴 방법
- 법인범용인증서가격
- 법인설립팁
- 법인범용인증서조달청
- 1인법인세무
- Today
- Total
이게뭐얔ㅋㅋ
수학 기호 정리 본문
i 아이. 허수단위. 제곱해서 -1이 되는 수.
√ 제곱근 또는 루트라고 읽습니다.
∫ 인테그랄 : 적분기호
± 플러스마이너스 : 플러스 또는 마이너스 라는 뜻
× 곱하기
÷ 나누기
≠ 같지 않다
∴ 따라서 또는 그러므로
∵ 왜냐하면
≒ 약, 근사값을 쓸때 또는 양쪽 값이 거의 비슷할때 사용
≤ (왼쪽이 오른쪽보다) 작거나 같다
≥ (왼쪽이 오른쪽보다) 크거나 같다
< (왼쪽이 오른쪽보다) 작다
> (왼쪽이 오른쪽보다) 크다
dθ 디쎄타, 미분에서 사용되는 기호입니다.
≡ 합동 또는 모듈로(mod)를 나타내는 기호=도형의 합동 기호
∈ (왼쪽이 오른쪽의) 원소이다.
∋ (오른쪽이 왼쪽의) 원소이다.
⊂ (왼쪽이 오른쪽의) 부분집합이다. (오른쪽 집합이 왼쪽 집합을) 포함한다.
⊃ (오른쪽이 왼쪽의) 부분집합이다. (오른쪽 집합이 왼쪽 집합을) 포함한다.
∪ 합집합
∩ 교집합
∀ 임의의
∃ 존재한다. exist.
ω(오메가) : x^2+x+1=0 을 만족시키는 x의 값
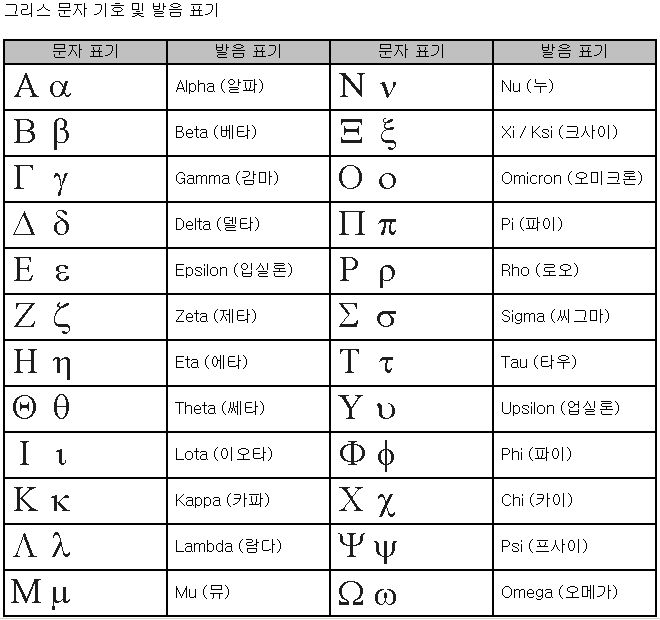
Α α →알파(ALPHA), Β β →베타(BETA), Γ γ →감마(GAMMA)
방정식의 근을 나타낼 대와 공간도형에서 평면, 방사선의 종류를 나타낼 때 쓰이기도 합니다.
Δ δ →델타(DELTA)
소문자는근을 나타낼 때 많이 쓰이고, 대문자는 미분의 변화량을 나타낼 때 주로 쓰입니다.
Ε ε →입실론(EPSILON)
소문자 형태는 극한을 엄밀하게 정의할 때, 아주 작은 미세한 값을 뜻할 때 주로 쓰입니다.
Θ θ →쎄타(THETA)
소문자는 주로 삼각함수에서 각을 나타낼 때 주로 쓰입니다.
Λ λ →람다(LAMBDA)
물리에서 주로 파장을 표현할 때 씁니다.
Μ μ →뮤(MU)
수학에서 모집단의 평균으로 많이 나타냅니다.
Ο ο →오미크론(OMICRON)
알파벳의 'o'와 비슷해서 거의 안 씁니다.
Π π →파이(PI)
소문자는 주로 원주율을 나타내고 대문자는 곱하기의 기호로 많이 씁니다.
Σ σ →시그마(SIGMA)
대문자는 더하기의 기호로 많이 쓰고, 소문자는 모집단의 표준편차를 많이 나타냅니다.
Φ φ →화이(PHI)
대문자는 주로 공집합을 표현하고 소문자는 함수로도 표현합니다.
출처
'삽질' 카테고리의 다른 글
| 애프터버너(after burner)로 채굴량 늘리기 (0) | 2021.05.19 |
|---|---|
| windows10 c++ builder personal 설치 (0) | 2017.06.05 |
| c++소스 에러 목록 (0) | 2016.03.11 |
| AVD 생성시 권한 문제 (0) | 2016.03.08 |
| openCV 카메라 및 1. 2. 버전 예제 문제 (0) | 2016.03.08 |
